Invented in 1957, by Frank Rosenblatt, the single layer perceptron network is the simplest type of neural network. The single layer perceptron network is able to act as a binary classifier for any linearly separable data set.
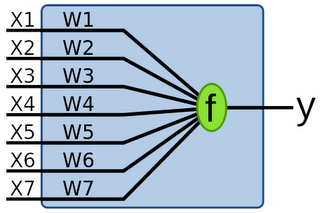
The SLP is nothing more than a collection of weights and an output value. The Clojure code below allows you to create a network (initially with zero weights) and get a result from the network given some weights and an input. Not very interesting.
(defn create-network
[out]
(repeat in 0))
(defn run-network
[input weights]
(if (pos? (reduce + (map * input weights))) 1 0))
The clever bit is adapting the weights so that the neural network learns. This process is known as training and is based on a set of data with known expectations. The learning algorithm for SLPs is shown below. Given an error (either 1 or -1 in this case), adjust the weights based on the size of the inputs. The
learning-rate decides how much to vary the weights; too high and the algorithm won't converge, too low and it'll take forever to converge.
(def learning-rate 0.05)
(defn- update-weights
[weights inputs error]
(map
(fn [weight input] (+ weight (* learning-rate error input)))
weights inputs))
Finally, we can put this all together with a simple training function. Given a series of samples and the expected values, repeatedly update the weights until the training set is empty.
(defn train
([samples expecteds] (train samples expecteds (create-network (count (first samples)))))
([samples expecteds weights]
(if (empty? samples)
weights
(let [sample (first samples)
expected (first expecteds)
actual (run-network sample weights)
error (- expected actual)]
(recur (rest samples) (rest expecteds) (update-weights weights sample error))))))
So we have our network now. How can we use it? Firstly, let's define a couple of data sets both linearly separable and not.
jiggle adds some random noise to each sample. Note the cool # syntax for a short function definition (I hadn't seen it before).
(defn jiggle [data]
(map (fn [x] (+ x (- (rand 0.05) 0.025))) data))
(def linearly-separable-test-data
[(concat
(take 100 (repeatedly #(jiggle [0 1 0])))
(take 100 (repeatedly #(jiggle [1 0 0]))))
(concat
(repeat 100 0)
(repeat 100 1))])
(def xor-test-data
[(concat
(take 100 (repeatedly #(jiggle [0 1])))
(take 100 (repeatedly #(jiggle [1 0])))
(take 100 (repeatedly #(jiggle [0 0])))
(take 100 (repeatedly #(jiggle [1 1]))))
(concat
(repeat 100 1)
(repeat 100 1)
(repeat 100 0)
(repeat 100 0))])
If we run these in the REPL we can see that the results are perfect for the linearly separable data.
> (apply train ls-test-data)
(0.04982859491606148 -0.0011851610388172009 -4.431771581539448E-4)
> (run-network [0 1 0] (apply train ls-test-data))
0
> (run-network [1 0 0] (apply train ls-test-data))
1
However, for the non-linearly separable they are completely wrong:
> (apply train xor-test-data)
(-0.02626745010362212 -0.028550312499346104)
> (run-network [1 1] (apply train xor-test-data))
0
> (run-network [0 1] (apply train xor-test-data))
0
> (run-network [1 0] (apply train xor-test-data))
0
> (run-network [0 0] (apply train xor-test-data))
0
The neural network algorithm shown here is really just a gradient descent optimization that only works for linearly separable data. Instead of calculating the solution in an iterative manner, we could have just arrived at an optimal solution in one go.
More complicated networks, such as the multi-layer perceptron network have more classification power and can work for non linearly separable data. I'll look at them next time!
Nice post. I'm novice in FP. Now I'm trying to play with Clojure. It's seems for me this paradigma is much closer to my way of thinking than OO. I was looking for any implementations of ANN on functional language. I'm planning to implement Restricted Boltzman Machine for humor and jokes extraction from text.
ReplyDeleteI'd like to know your opinion regarding using functional programming vs OO programming for ANN construction. Which one is better suited for this kind of tasks. As soon as I know with FP it is much simpler to programm for multiprocessor hardware. But how about memory consumption. With BP algorithm we should create many matrix copy when adjusting wheights.
So anybody using FP languages for ANN?
I'm definitely not an expert in FP or ANN so take this with a pinch of salt!
ReplyDeleteI think your concerns about many matrix copies are (probably) unfounded. The Clojure data structures are designed to mutate efficiently; they share the structure that stays the same only the new data changes. In addition, when you need to mutate you can do so in a safe way using transient.
Even if it is a little slower then you can probably win in the end with multi-processor support!
What is your opinion, the structure of typiclal NN can be best described from the point of view objects or functions?
ReplyDeleteAnd what structure would be better to use for NN structure, weights, inputs.
list
set
vectors
maps
or maybe use Java's structure?
"train" function does look a lot like reduce so I thought it'd be nice if you made test data 'reducable' and refactor "train" into function that may be used by "reduce".
ReplyDeleteYou can find source code at:
http://gist.github.com/402257
Thanks Paweł - that looks much cleaner!
ReplyDeleteLooking back now, I'm of the opinion anything that uses recur is almost certainly something you can do with a standard function. I guess recursion is a code smell in a functional language since most likely you can express it in terms of a map / fold operation.