Most of the exercises at the end of Chapter 3 of
Real World Haskell are fairly simple. Find the height of a list, verify a list is a palindrome and so on. The last few however are pretty tough..
The
convex hull is the smallest set of points that contain all the other points in the set. The image below from Wikipedia is a much better visual description:
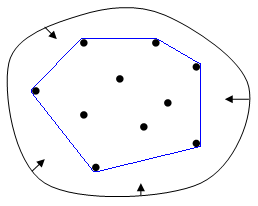
One approach for finding the convex hull is the
Graham Scan algorithm and this is the challenge presented in the book. The algorithm can be broken down into the following steps:
- Find the minimum point (with the lowest Y co-ordinate). In the event of a tie, the lowest x co-ordinate determines the minimum. Call this point P.
- Sort the remaining points relative to the angle formed by point and P relative to the x-axis.
- Consider each point in the sequence. For each point, determine whether it is a left turn or a right turn relative to the previous two points. If it is a "right turn" the second to last point is not in the convex hull. Continue until the list is finished.
To solve this, we'll declare some data structures which should be self explanatory.
data Direction = Straight
| LeftTurn
| RightTurn
deriving (Show)
data Point = Point Double Double
deriving (Show,Eq)
Next we define a function that calculates the turn made by three points and returns a Direction. We don't need to calculate the actual angle as the cotangent is proportional to the angle.
cross :: Point -> Point -> Point -> Double
cross (Point x1 y1) (Point x2 y2) (Point x3 y3) = ((x2-x1)*(y3-y1)-(x3-x1)*(y2-y1))
dist :: Point -> Point -> Double
dist (Point x1 y1) (Point x2 y2) = sqrt((x1-x2)^2 + (y1-y2)^2)
turn :: Point -> Point -> Point -> Direction
turn a b c = makeDirection (cross a b c) where
makeDirection x | x == 0 = Straight
| x < 0 = LeftTurn
| x > 0 = RightTurn
In order to find the minimum Point and sort the list we need to define two comparator functions for use with sortBy and minimumBy (both members of Data.List).
compareYPoint :: Point -> Point -> Ordering
compareYPoint (Point x1 y1) (Point x2 y2)
| y1 == y2 = compare x1 x2
| y1 <= y2 = LT
| otherwise = GT
compareCross :: Point -> Point -> Point -> Ordering
compareCross pvt a b = if (angle == EQ) then distance else angle where
angle = compare (cross pvt a b) 0
distance = compare (dist pvt a) (dist pvt b)
Even though compareCross takes 3 arguments, we can still use this as type
Point -> Point -> Ordering by using currying.
lowestY :: [Point] -> Point
lowestY = minimumBy compareYPoint
grahamScan :: [Point] -> [Point]
grahamScan points = undefined where
p = nub points
pvt = lowestY p
sortedPoints = pvt : (sortBy (compareCross pvt) (delete pvt p))
nub is a function that removes duplicate elements from a list. This gives the skeleton of the program. Now we have to do the complicated bit. From Wikipedia:
The algorithm proceeds by considering each of the points in the sorted array in sequence. For each point, it is determined whether moving from the two previously considered points to this point is a "left turn" or a "right turn". If it is a "right turn", this means that the second-to-last point is not part of the convex hull and should be removed from consideration. This process is continued for as long as the set of the last three points is a "right turn". As soon as a "left turn" is encountered, the algorithm moves on to the next point in the sorted array
Let's take the simplest example possible. For the following points (0,0), (2,0), (2,2), (0,2), (1,1) the convex hull should be everything apart from (1,1).

In order to check how this is going to work, we need to define a quick helper function to make building lists of Point types less verbose.
pointsFromTupleList :: [(Double,Double)] -> [Point]
pointsFromTupleList = map (\(x,y) -> Point x y)
examplePoints :: [Point]
examplePoints = pointsFromTupleList [(0,0),(2,0),(2,2),(0,2),(1,1)]
Now we can explore the functions that we're going to use and verify they work
-- The minimum point appears correct
*Main> lowestY examplePoints
Point 0.0 0.0
-- The points are sorted as expected
*Main> let sortedPoints = (Point 0 0):(sortBy (compareCross (Point 0 0)) (delete (Point 0 0) examplePoints))
*Main>sortedPoints
[Point 0.0 0.0,Point 0.0 2.0,Point 1.0 1.0,Point 2.0 2.0,Point 2.0 0.0]
The next task is to calculate the turns made.
*Main> getTurns sortedPoints
[LeftTurn,RightTurn,LeftTurn]
That's not much use because I don't know the points which constitute the turns. Let's tuple up the results:
getTurns :: [Point] -> [((Point,Point,Point),Direction)]
getTurns (x:y:z:ps) = ((x,y,z),turn x y z) : getTurns (y:z:ps)
getTurns _ = []
*Main> getTurns sortedPoints
[((Point 0.0 0.0,Point 0.0 2.0,Point 1.0 1.0),LeftTurn),
((Point 0.0 2.0,Point 1.0 1.0,Point 2.0 2.0),RightTurn),
((Point 1.0 1.0,Point 2.0 2.0,Point 2.0 0.0),LeftTurn)]
The algorithm states that I should ignore the second to last parameter if it is a right turn, and keep it otherwise. Clearly we're close here because the second to last parameter for a right turn is the only point not in the convex hull. One problem with the sortedPoints is that we're not returning to where we started. Let's change the definition again so that we can get back to where we started. We add two nodes at the end so that the extra padding means we consider all triplets
sortedPoints = pvt : (sortBy (compareCross pvt) (delete pvt p)) ++ [pvt,pvt]
*Main> getTurns sortedPoints
[((Point 0.0 0.0,Point 0.0 2.0,Point 1.0 1.0),LeftTurn),
((Point 0.0 2.0,Point 1.0 1.0,Point 2.0 2.0),RightTurn),
((Point 1.0 1.0,Point 2.0 2.0,Point 2.0 0.0),LeftTurn),
((Point 2.0 2.0,Point 2.0 0.0,Point 0.0 0.0),LeftTurn),
((Point 2.0 0.0,Point 0.0 0.0,Point 0.0 0.0),Straight)]
So now all I need to do to solve the problem is keep the middle point in all cases where we've got a LeftTurn or Straight. I can simplify this further by just only getting the middle point in the tuple.
getTurns :: [Point] -> [Point,Direction)]
getTurns (x:y:z:ps) = (y,turn x y z) : getTurns (y:z:ps)
getTurns _ = []
grahamScan :: [Point] -> [Point]
grahamScan points = map fst (filter (\(x,d) -> d /= RightTurn) (getTurns sortedPoints)) where
p = nub points
pvt = lowestY p
sortedPoints = pvt : (sortBy (compareCross pvt) (delete pvt p)) ++ [pvt,pvt]
-- Hurrah, it finally works (for this one example).
*Main> grahamScan examplePoints
[Point 0.0 2.0,Point 2.0 2.0,Point 2.0 0.0,Point 0.0 0.0]
One example works, that'll do me as I've learnt enough from this exercise to make it worthwhile. I strongly suspect the way I'm extending the point list by appending the pivot twice at the end is just a hack rather than the right way. There's another definition
here which looks cleaner, but that apparently has some issues too.
The complete code looks like this. hlint was run on this and pointed out the "uncurry" function which converts a curried function to a function on pairs. This simplifies the definition of
pointsFromTupleList.
data Direction = Straight
| LeftTurn
| RightTurn
deriving (Show,Eq)
data Point = Point Double Double
deriving (Show,Eq)
turn :: Point -> Point -> Point -> Direction
turn a b c = makeDirection (cross a b c) where
makeDirection x | x == 0 = Straight
| x < 0 = LeftTurn
| x > 0 = RightTurn
cross :: Point -> Point -> Point -> Double
cross (Point x1 y1) (Point x2 y2) (Point x3 y3) = (x2-x1)*(y3-y1)-(x3-x1)*(y2-y1)
dist :: Point -> Point -> Double
dist (Point x1 y1) (Point x2 y2) = sqrt((x1-x2)^2 + (y1-y2)^2)
compareCross :: Point -> Point -> Point -> Ordering
compareCross pvt a b = if angle == EQ then distance else angle where
angle = compare (cross pvt a b) 0
distance = compare (dist pvt a) (dist pvt b)
getTurns :: [Point] -> [(Point,Direction)]
getTurns (x:y:z:ps) = (y,turn x y z) : getTurns (y:z:ps)
getTurns _ = []
grahamScan :: [Point] -> [Point]
grahamScan points = map fst (filter (\(x,d) -> d /= RightTurn) (getTurns sortedPoints)) where
p = nub points
pvt = lowestY p
sortedPoints = pvt : sortBy (compareCross pvt) (delete pvt p) ++ [pvt,pvt]
compareYPoint :: Point -> Point -> Ordering
compareYPoint (Point x1 y1) (Point x2 y2)
| y1 == y2 = compare x1 x2
| y1 <= y2 = LT
| otherwise = GT
compareAngle :: Point -> Point -> Point -> Ordering
compareAngle (Point px py) p1 p2 = compare (angle p2) (angle p1) where
angle (Point x1 y1) = y1-py / x1-px
lowestY :: [Point] -> Point
lowestY = minimumBy compareYPoint
pointsFromTupleList :: [(Double,Double)] -> [Point]
pointsFromTupleList = map (uncurry Point)
examplePoints :: [Point]
examplePoints = pointsFromTupleList [(0,0),(2,0),(2,2),(0,2),(1,1)]



