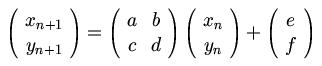(just some notes as I plunder
online tutorials to get the information I want on the most basic parts of Haskell).
Haskell's REPL is the
ghci tool. It works in a similar manner to
Clojure's. The "Prelude" prefix indicates the module that we are currently in (similar to the namespace idea in Clojure).
Prelude is the standard Haskell library consisting of standard definitions for various types and functions.
:? (or
:help) gives help on the available commands in the REPL. The most useful I've found so far are:
Haskell uses infix (compared to Lisp's prefix) notation (though you can enclose an operator with parenthesis and make it prefix (e.g. (+) 1 1 is 2). A type is named with an initial capital letter, for example Boolean values use
True and
False. C style &&, == and || operators are used and do exactly what you'd expect! != is written /=.
The list data structure in Haskell is created using square brackets ([]). The biggest difference between this and Lisp lists is that the items in the list must be of the same type. For example, lists of numbers are fine but mixing numbers and characters is forbidden (tuples are the solution to this).
Prelude> :type [1,2]
[1,2] :: (Num t) => [t]
Prelude> :type [1,2.0]
[1,2.0] :: (Fractional t) => [t]
Prelude> :type [1.0,2.0]
[1.0,2.0] :: (Fractional t) => [t]
Prelude> :type [1,"a"]
:1:1:
No instance for (Num [Char])
arising from the literal `1' at :1:1
head and
tail can be used to get (as you'd expect) the first and rest of the list (car / cdr) (
head [1,2,3] ==> 1, tail [1,2,3] ==> [2,3]). Performing head/tail on an empty list raises an exception.
++ is for appending lists together (
[1,2,3] ++ [4,5,6] ==> [1,2,3,4,5,6]). The number of items in a list can be determined using
length. A range of numbers can be created with the
.. notation (e.g.
[1..5] ==> [1,2,3,4,5]). If the first two elements are provided then this gives the "step" for the range (e.g.
[1,3..10] ==> [1,3,5,7,9]).
To define functions within GHCI, use let to introduce a name.
Prelude> let myadd x y = x + y
Prelude> myadd 7 14
21
This doesn't scale very nicely (you have to use
:{ and :} directives in order to have a multiple line function), so the preferred way is to put it in a file and use
:load to bring it in. Note that the function is compiled as it is loaded.
Another key feature of Haskell is pattern matching. Multiple function definitions can be written and the body is executed for the pattern that it matches. For example, we can define our own length function as:
mylength [] = 0
mylength (x:xs) = 1 + mylength xs
This is a recursive function, so what happens to the stack? Running mylength [1..10000000000] results in a stack overflow, why's that? This is because of laziness and is covered in detail
here. The problem is that because Haskell is a lazy language the computation is only evaluated when needed, this builds up a giant "thunk" (pending computations) for all the items in the list which in turn requires them to all be in memory. Laziness is
hard to reason about - practise will make perfect.
List comprehensions provide a way for a list to be generated from a series of functions. In the example below <- is a generator function meaning use one of these values to substitute in for each value.
Prelude> [(x,y) | x <- [1,2,3], y <- [4,5,6]]
[(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6)]
List comprehensions are evaluated left to right, so in the example above x is fixed until all values of y have been exhausted. Hence don't make y an infinite range otherwise it'll never get to the next value of x...
Next on the list, exploring the basics of types!