Iterated Function Systems

An Iterated Function System (IFS) is a technique for creating fractal images. The name comes from the simple way in which they work. Start at an arbitrary point and colour it in, perform a transformation of that point to some new point. Colour that in and repeat until done. The translation function typically chooses between one of any number of choices. This is also called the Chaos Game.

The classic example if the Sierpinski Triangle (which incidentally has a much cooler Clojure implementation [using a different technique] in 3d here). My 2D rendering kind of pales in comparison!



This flavour of IFS is generated using a simple two dimensional affine transform. (this limits it to scale, rotation and translation, but not shearing transforms). The equation for this is shown below:



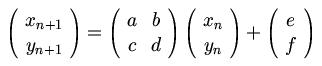
An implementation of this in Clojure is shown below. The formula above is expanded out in calculate-point



The second example draws a simple fern leaf pattern known as Barnsley's Fern.



The code to do the rendering uses a single agent to provide the animation (by repeatedly setting individual pixels). It's a bit yucky because I've no idea how to check the bounds of an arbitrary set of functions, so I make a guess by checking the first 10000 values to get an idea of min/max (get-bounds). The ugliness is compounded by the floor, abs and inc strategically located which get around the rounding errors. (big thanks to Hoeck from #clojure who suggested using take-while instead of the hideous gumph I had before which threw an exception to abort).



Obviously the time taken is dependent on how many equations are used, but images are generated very quickly. The get-bounds function on my box computes 10000 iterations of the Sierpinski set in 30 ms!

Full code available here in the misc folder.